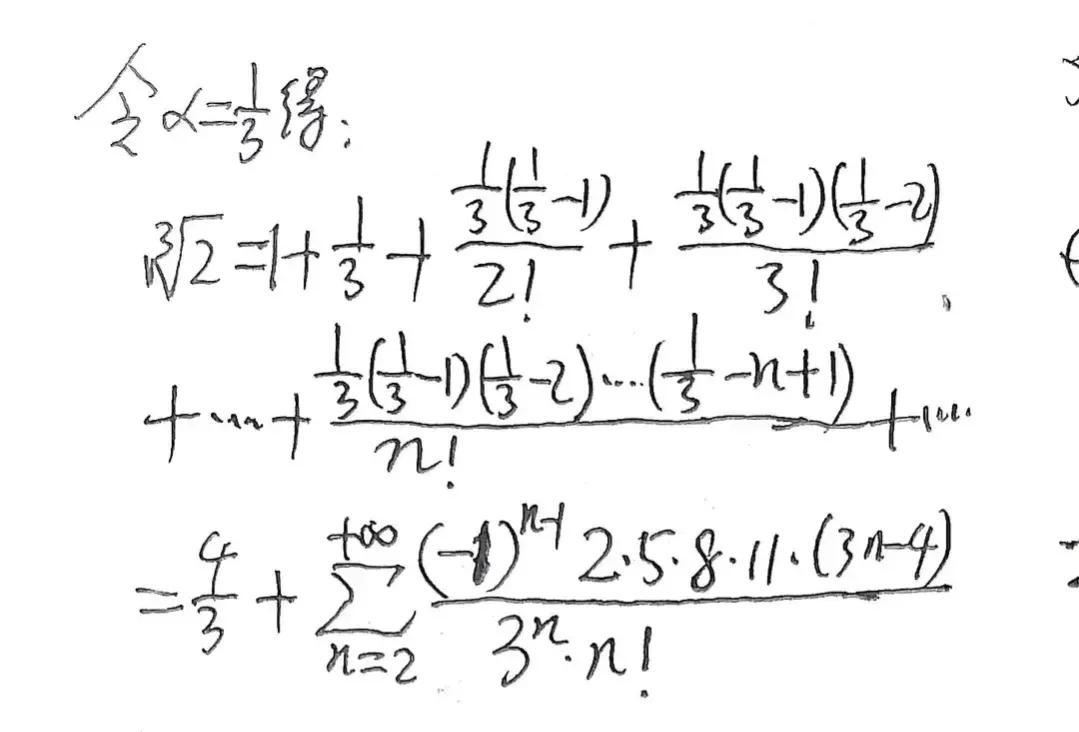数学世界里充满了奇妙的对称关系。反函数求导就是这样一个体现——当我们知道原函数的导数时,如何求出它的反函数的导数。这个概念在微积分中占据着重要位置,它像一座桥梁,连接着两个看似不同却紧密相关的函数。
1.1 反函数的定义与性质
反函数本质上是一种“逆向操作”。如果函数f把x映射到y,那么它的反函数f⁻¹就把y映射回x。简单来说,反函数就是原函数的“倒带按钮”。
举个例子,温度转换就是个很好的例子。摄氏转华氏的公式是F = 1.8C + 32,它的反函数就是华氏转摄氏:C = (F - 32)/1.8。这两个函数互为反函数,一个负责“去”,一个负责“回”。
反函数有几个关键特性值得注意。它们关于直线y = x对称——这个性质在图像上表现得特别明显。如果你把原函数图像沿着y=x线对折,就会得到反函数的图像。另一个重要性质是f(f⁻¹(x)) = x,就像你出门又回家,最终回到了起点。
我记得第一次在坐标纸上画出y=x²和它的反函数y=√x时的惊讶。两条曲线完美对称,就像镜子里外的世界。
1.2 反函数存在的条件
不是所有函数都有反函数。要让反函数存在,原函数必须是一一对应的。这意味着每个x值对应唯一的y值,同时每个y值也对应唯一的x值。
水平线测试是个很实用的判断方法。如果在函数图像上,任何水平线最多只与图像相交一次,那么这个函数就有一一对应的性质,它的反函数存在。
单调函数通常满足这个条件。比如y = x³在整个实数范围内单调递增,它的反函数y = ∛x就处处存在。但y = x²在全体实数上就不行,因为除了零以外的正数y都对应两个x值。
有时候我们可以通过限制定义域来“创造”反函数。y = x²在x ≥ 0时就有反函数y = √x。这种处理方式在实际应用中很常见。
1.3 反函数与原函数的关系
反函数和原函数之间存在着深刻的联系。它们的导数互为倒数——这个关系简洁而优美。如果y = f(x)在某个点可导,且f'(x) ≠ 0,那么它的反函数x = f⁻¹(y)在该对应点也可导,且导数满足[f⁻¹(y)]' = 1/f'(x)。
用更直观的方式理解:原函数陡峭的地方,反函数就平缓;原函数平缓的地方,反函数就陡峭。它们像一对默契的舞伴,一个进,一个退。
这种关系在具体计算中特别有用。当我们遇到复杂函数的反函数求导时,不需要从头开始推导,直接利用这个倒数关系就能得到结果。它大大简化了计算过程,让原本复杂的问题变得简单明了。
反函数求导的基本概念为我们后续的学习打下了坚实基础。理解这些核心思想,后面的公式推导和应用就会水到渠成。
掌握了反函数的基本概念后,我们来看看具体的求导公式是怎么来的。这个推导过程本身就很迷人——它展示了微积分中不同概念如何巧妙地交织在一起。我特别喜欢这种从已知推导未知的思考方式,就像解开一个精心设计的数学谜题。
2.1 隐函数求导法推导
隐函数求导法提供了一条优雅的路径来推导反函数求导公式。我们从最基本的关系开始:如果y = f(x),那么它的反函数就是x = f⁻¹(y)。
现在假设f在点x可导,我们想求f⁻¹在对应点y的导数。考虑恒等式f(f⁻¹(y)) = y,这个等式表达了反函数的本质特性——原函数和反函数相互“抵消”。
对这个恒等式两边关于y求导,左边用链式法则,右边直接求导: f'(f⁻¹(y)) · [f⁻¹(y)]' = 1
这里f'(f⁻¹(y))就是f在点x = f⁻¹(y)处的导数,记作f'(x)。于是我们得到: f'(x) · [f⁻¹(y)]' = 1
整理后得到反函数求导公式: [f⁻¹(y)]' = 1/f'(x)
这个推导的简洁性令人赞叹。它不需要复杂的计算,只用了隐函数求导的基本思想。我记得第一次看到这个推导时,那种“原来如此”的顿悟感至今难忘。
2.2 链式法则推导
链式法则给出了另一种推导视角,可能更直观一些。我们从微分角度考虑这个问题。
设y = f(x)有反函数x = g(y),那么有恒等式: y = f(g(y))
两边对y求导,应用链式法则: 1 = f'(g(y)) · g'(y)
因为g(y)就是f⁻¹(y),所以: 1 = f'(f⁻¹(y)) · [f⁻¹(y)]'
重新整理得到: [f⁻¹(y)]' = 1/f'(f⁻¹(y))
注意到f⁻¹(y) = x,所以: [f⁻¹(y)]' = 1/f'(x)
这个推导强调了链式法则在连接原函数与反函数时的桥梁作用。它清晰地展示了为什么反函数的导数恰好是原函数导数的倒数——因为它们的微分效果必须相互抵消。
2.3 几何直观解释
几何视角让这个公式变得生动起来。想象一下原函数y = f(x)和它的反函数x = f⁻¹(y)的图像,它们关于直线y = x对称。
在原函数图像上,某点的切线斜率是f'(x)。在反函数图像上,对应的点是通过原图像关于y = x对称得到的,所以切线的斜率会发生变化。
具体来说,如果原函数在某点的切线斜率为m,那么反函数在对应点的切线斜率就是1/m。这个关系可以从对称性直接看出来——当图像关于y = x对称时,切线的“陡峭程度”会互相补充。
更精确地说,假设原函数在点(a, b)的切线斜率为m,那么这条切线关于y = x对称后,就变成了反函数在点(b, a)的切线,其斜率正好是1/m。
这种几何解释不仅直观,还帮助我们理解为什么要求f'(x) ≠ 0。如果原函数的切线水平(斜率为0),那么反函数的切线就会变成垂直(斜率无穷大),这在导数定义中是不允许的。
看着函数图像,你能真切感受到原函数陡峭时反函数平缓,原函数平缓时反函数陡峭的互补关系。这种视觉上的理解往往比纯代数推导更加深刻。
反函数求导公式的推导展示了数学中不同思维方式的美妙统一。代数推导给出精确结果,几何解释提供直观理解,它们共同构成了对这个重要公式的完整认识。
理解了反函数求导公式的推导后,我们来看看如何在实际问题中灵活运用这个工具。应用技巧的关键在于把握公式的本质——反函数的导数等于原函数导数的倒数,同时注意变量的对应关系。这种对应关系在实际计算中常常是容易出错的地方。
3.1 常见反函数的求导实例
从最基本的反三角函数开始,这些函数在工程和物理中频繁出现。以反正弦函数为例,设y = arcsin x,那么原函数就是x = sin y。
根据反函数求导公式: (arcsin x)' = 1/(sin y)' = 1/cos y
但这里有个细节需要注意——我们需要用x来表示cos y。根据sin²y + cos²y = 1,得到cos y = √(1 - sin²y) = √(1 - x²)。考虑到arcsin x的值域是[-π/2, π/2],在这个区间内cos y ≥ 0,所以: (arcsin x)' = 1/√(1 - x²)
类似地,对于反余弦函数y = arccos x: (arccos x)' = 1/(cos y)' = 1/(-sin y) = -1/√(1 - x²)
我教微积分时发现,学生经常忘记这里的负号。其实从几何角度很好理解——arcsin是递增函数,导数应为正;arccos是递减函数,导数自然为负。
对数函数作为指数函数的反函数也很有趣。设y = ln x,原函数是x = eʸ: (ln x)' = 1/(eʸ)' = 1/eʸ = 1/x
这个结果的简洁性令人惊叹。我记得第一次意识到对数函数的导数如此简单时,那种数学之美带来的震撼至今记忆犹新。
3.2 复合反函数的求导方法
实际问题中经常遇到反函数与其他函数复合的情况,这时链式法则就派上用场了。关键在于分清层次——先处理外层函数,再处理内层的反函数。
考虑y = arctan(√x),这是一个复合函数,外层是arctan,内层是√x。用链式法则: y' = [arctan(√x)]' = 1/(1 + (√x)²) · (1/(2√x))
化简后得到: y' = 1/(2√x(1 + x))
另一个例子是y = ln(arcsin x)。这里外层是ln函数,内层是arcsin函数: y' = [1/arcsin x] · [1/√(1 - x²)]
这种复合结构在概率论和统计中很常见,特别是在处理变换后的随机变量时。我处理过一个信号处理的问题,其中就涉及到类似的双重反函数结构,当时如果没有理清这个层次关系,计算就会变得一团糟。
3.3 参数方程中的反函数求导
参数方程形式x = φ(t), y = ψ(t)在描述曲线时非常有用。当我们需要求dy/dx时,如果直接关系复杂,反函数求导就能发挥作用。
标准做法是: dy/dx = (dy/dt)/(dx/dt) = ψ'(t)/φ'(t)
但有时候我们可能需要dx/dy,这时: dx/dy = (dx/dt)/(dy/dt) = φ'(t)/ψ'(t)
这个结果其实就是反函数求导公式的参数形式。因为如果y是x的函数,那么x也可以看作是y的函数(在局部),它们的导数互为倒数。
考虑一个具体例子:摆线的参数方程x = a(t - sin t), y = a(1 - cos t)。求在t = π/2处的dy/dx和dx/dy。
先求导数: dx/dt = a(1 - cos t), dy/dt = a sin t
在t = π/2时: dx/dt = a(1 - 0) = a, dy/dt = a·1 = a
所以: dy/dx = (a)/(a) = 1 dx/dy = (a)/(a) = 1
这个结果说明在t = π/2处,曲线相对x轴和y轴的倾斜程度相同。参数方程求导的美妙之处在于它绕过了显式表达y = f(x)的困难,直接通过参数t建立联系。
反函数求导的应用技巧核心在于灵活转化视角。有时候直接求导困难,转换成反函数问题反而迎刃而解。这种思维方式在解决复杂问题时特别有用——正面攻不破,就换个角度试试。
数学公式的真正魅力在于它能解决现实世界中的具体问题。反函数求导这个看似抽象的工具,在物理实验室、经济模型和工程设计中都有着生动的应用场景。当你看到这些公式如何描述物体运动、分析市场行为、优化系统性能时,会感受到理论知识与实际问题的深刻连接。
4.1 物理学中的运动学问题
运动学中经常需要从位置求速度,或者反过来从速度求位置——这种互逆关系天然适合用反函数求导来处理。
考虑一个竖直上抛的物体,它的高度随时间变化关系为h(t) = 20t - 5t²。如果我们想知道物体达到某一高度时的瞬时速度,直接求解可能比较麻烦。但利用反函数思想,设t是h的函数,那么速度v = dh/dt,而dt/dh = 1/v。
当h = 15米时,解方程15 = 20t - 5t²得到t = 1秒或3秒。计算导数dh/dt = 20 - 10t,在t=1时v=10 m/s向上,t=3时v=-10 m/s向下。通过反函数求导,dt/dh = 1/(20-10t),我们得到了时间关于高度的变化率。
我在大学物理实验里测量过弹簧振子的运动,当时就用到了类似的方法。我们记录了振子通过平衡位置的时间,想要找出位移与时间的精确关系。直接拟合数据很困难,但通过考虑时间的反函数,问题变得清晰很多。
另一个典型例子是行星运动中的开普勒问题。已知行星的角位置随时间变化的关系,求特定位置对应的时刻。这种轨道力学问题在航天工程中至关重要,反函数求导提供了有效的数值解法基础。
4.2 经济学中的边际分析
经济学中的边际概念本质上就是导数,而许多经济关系天然具有相互性,适合用反函数来处理。
需求函数Q = D(P)表示在价格P时的需求量,它的反函数P = D⁻¹(Q)就是反需求函数,表示为了卖出Q单位商品需要的价格。需求弹性ε = (dQ/dP)·(P/Q),但有时候我们更关心价格对数量的敏感度,这时就需要dP/dQ = 1/(dQ/dP)。
假设某商品的需求函数为Q = 100 - 2P,那么dQ/dP = -2。当Q = 60时,P = 20,此时dP/dQ = -1/2。这意味着数量每增加1单位,价格需要下降0.5单位来维持市场出清。
我记得分析过一个电商平台的销售数据,想要找出最优定价策略。直接建立价格与销量的关系很复杂,但通过考虑销量的反函数,我们发现了更有趣的模式——在某些销量区间,价格敏感度会发生突变,这对应着不同的消费者群体。
在成本分析中,如果已知成本C是产量Q的函数C(Q),那么平均成本最小时满足d(C/Q)/dQ = 0。通过变换,这个条件可以转化为关于Q的反函数问题,往往能提供更直观的经济解释。
4.3 工程学中的优化问题
工程设计本质上是在各种约束下寻找最优解,反函数求导在优化算法和敏感性分析中扮演着关键角色。
在结构力学中,经常需要建立载荷与变形的关系。比如梁的挠度δ与载荷P的关系可能是δ = kPⁿ,那么反函数P = (δ/k)^(1/n)给出了产生特定挠度所需的载荷。导数dP/dδ表示刚度——结构抵抗变形的能力。
考虑一个具体的例子:设计一个悬臂梁,要求最大挠度不超过δ_max。已知δ = PL³/(3EI),其中E是弹性模量,I是惯性矩。那么P = (3EI/L³)δ,dP/dδ = 3EI/L³。这个导数告诉我们,梁的刚度与EI成正比,与长度的立方成反比。
我参与过一个机器人臂的设计项目,需要优化各个关节的扭矩分配。直接建立位置到扭矩的映射很困难,但我们通过考虑反函数——从期望的末端执行器位置反推各关节角度,再计算所需扭矩——使得优化问题变得可解。这种逆向思维在运动规划中非常有效。
在控制系统设计中,经常需要从系统的响应反推参数设置。比如已知系统的阶跃响应曲线,想要确定PID控制器的参数。这本质上是一个反函数求导问题,现代优化算法如梯度下降法就大量运用了这种思想。
反函数求导在实际应用中更像是一种思维方式——当直接路径受阻时,考虑反向路径可能柳暗花明。这种双向思考的能力,是区分优秀工程师、物理学家和经济学家的关键。
当我们在单变量函数的领域里熟练掌握了反函数求导,很自然地会想:如果面对的是更复杂的多元函数呢?如果函数关系不是显式给出的呢?这些问题将我们带向微积分的更深层领域。反函数求导的思想在这里不仅没有消失,反而以更丰富的形式继续发挥着作用。
5.1 多元函数的反函数求导
从一元到多元,反函数求导的概念需要升级为更强大的工具——雅可比矩阵。这不再是单个导数的倒数关系,而是矩阵的逆运算。
考虑一个从R²到R²的映射:u = f(x,y), v = g(x,y)。如果这个映射存在反函数x = φ(u,v), y = ψ(u,v),那么导数关系通过雅可比矩阵来描述。原映射的雅可比矩阵是:
J = [∂f/∂x ∂f/∂y; ∂g/∂x ∂g/∂y]
而反函数的雅可比矩阵恰好是J的逆矩阵。这个结论优美地推广了一元情形中的[dx/du = 1/(du/dx)]。
我在数值计算课程中第一次接触这个概念时,被它的几何直观深深吸引。想象两个平面之间的光滑映射,局部来看,它就像一个线性变换。反函数定理保证了在非奇异的点附近,这个变换是可逆的——就像你可以把一块橡皮泥平滑地变形,然后再恢复原状。
一个具体的例子:极坐标变换x = r cosθ, y = r sinθ。它的雅可比矩阵是[cosθ -r sinθ; sinθ r cosθ],行列式为r。当r≠0时,反变换r = √(x²+y²), θ = arctan(y/x)存在,其雅可比矩阵正好是原矩阵的逆。
多元反函数求导在物理场论中特别有用。比如在流体力学中,我们经常需要在欧拉描述和拉格朗日描述之间转换——本质上就是在不同坐标系间寻找反函数关系。
5.2 隐函数定理与反函数定理
隐函数定理是多元微积分中的明珠,它告诉我们:即使不能显式解出反函数,反函数仍然局部存在。这个定理为反函数求导提供了坚实的理论基础。
定理的核心思想很直观:如果F(x,y) = 0,且∂F/∂y ≠ 0,那么在(x₀,y₀)附近,方程F(x,y)=0唯一确定了一个函数y=f(x)。更重要的是,我们可以求出它的导数dy/dx = - (∂F/∂x)/(∂F/∂y),而不需要显式解出y。
反函数定理是隐函数定理的特例。如果要判断映射y=f(x)是否局部可逆,只需要检查f'(x₀)是否可逆(在多元情形就是雅可比矩阵是否满秩)。这个条件如此简洁,却蕴含着深刻的结果。
我第一次真正理解这个定理是在研究机器人运动学的时候。机械臂的末端位置由各关节角度决定,我们想知道:给定末端的一个微小移动,各关节需要如何调整?这正好是反函数定理的应用——只要雅可比矩阵满秩,就存在局部的反函数关系。
隐函数定理在经济学中也有精彩应用。考虑一个简单的市场均衡模型:D(p,y)=S(p)定义了一个隐函数关系。即使不能显式解出价格p作为收入y的函数,我们仍然可以分析dp/dy = - (∂D/∂y)/(∂D/∂p - dS/dp),从而理解收入变化对均衡价格的影响。
这些定理的价值在于,它们让我们在无法获得显式解的情况下,仍然能够进行定性和定量的分析。
5.3 反函数求导在机器学习中的应用
机器学习可以看作是在高维空间中寻找复杂函数的反函数。从生成模型到强化学习,反函数求导的思想以各种形式出现。
生成对抗网络(GAN)的核心就是学习一个从简单分布到复杂数据分布的变换。生成器实际上是在实现一个反函数——从潜空间中的随机向量生成逼真的数据样本。训练过程中需要计算这种复杂变换的导数,这本质上就是反函数求导在高维空间的推广。
标准化流模型则更加直接地运用了反函数求导。这些模型通过一系列可逆变换将简单分布转换为复杂分布。因为每个变换都是可逆的,所以可以精确计算数据的似然概率。这里的关键是每个变换的雅可比矩阵必须容易计算(或者至少容易计算其行列式)。
我尝试过用标准化流模型生成手写数字,那些可逆的神经网络层确实令人惊叹。它们像是一连串精心设计的坐标变换,把杂乱无章的噪声变成有意义的图案。训练过程中,我们需要计算从潜变量到数据点的变换的雅可比行列式——这正好是反函数求导的高维版本。
在强化学习中,逆强化学习试图从专家的行为反推奖励函数。这可以理解为:已知最优策略(行为),求导致这种策略的奖励函数。虽然不是严格数学意义上的反函数,但思想是相通的——从结果反推原因。
深度学习中的自动微分技术让这些复杂的求导计算成为可能。无论是正向传播还是反向传播,都涉及函数与反函数的导数计算。现代机器学习框架如PyTorch和TensorFlow,本质上都是在高效地计算这些导数关系。
反函数求导的拓展告诉我们,数学思想具有惊人的延续性。从一元函数的简单倒数关系,到多元函数的矩阵求逆,再到机器学习中的可逆神经网络,核心的逆向思维始终在发光发热。这种从已知探寻未知、从结果反推原因的能力,正是人类智能的独特优势。